![[Algorithm] DFS, BFS](https://www.freelancinggig.com/blog/wp-content/uploads/2019/02/BFS-and-DFS-Algorithms.png)
[Algorithm] DFS, BFS
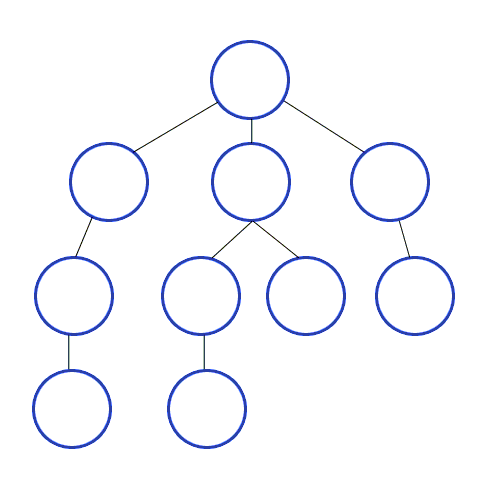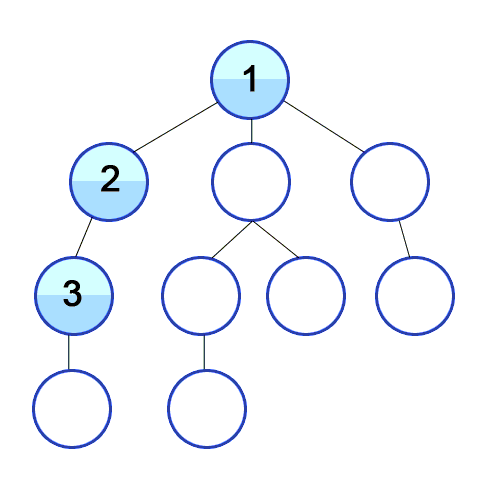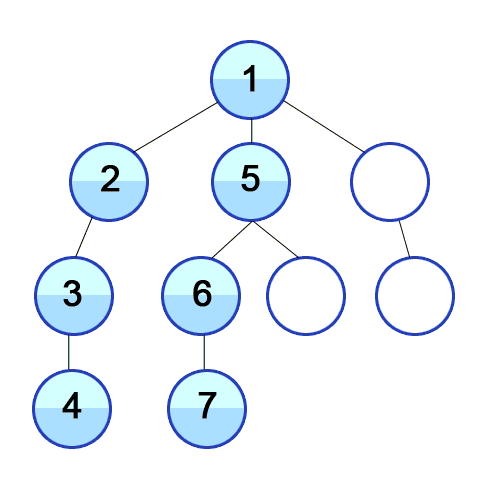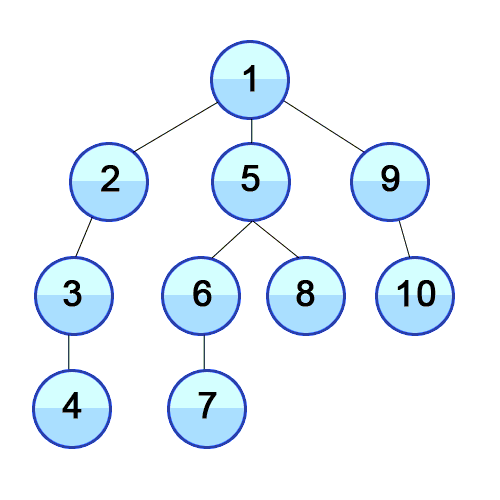
깊이 우선 탐색 (DFS)
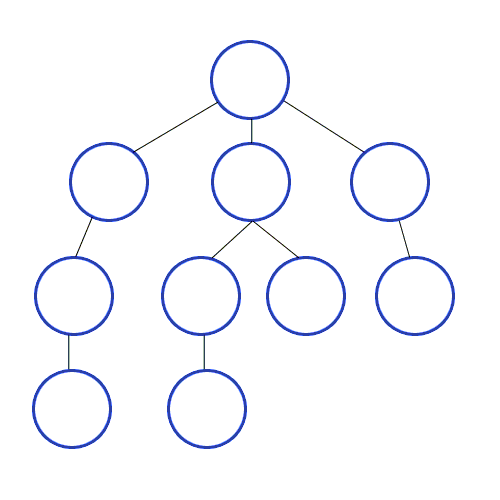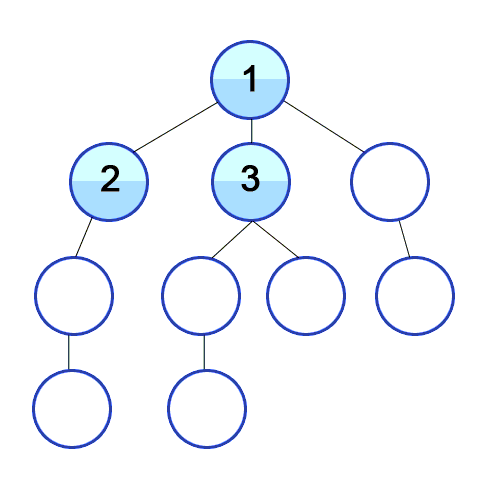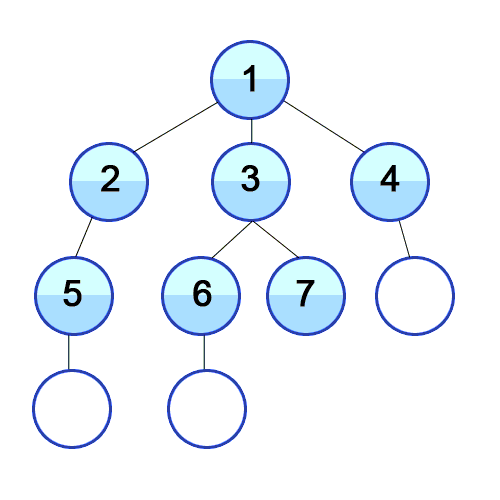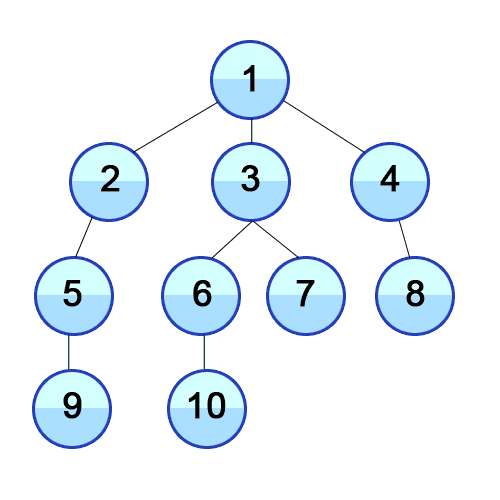
깊이 우선 탐색은 현재 노드에서 갈 수 있는 한 깊이까지 내려가며 탐색을 진행한 후, 더 이상 내려갈 곳이 없으면 바로 이전 단계로 되돌아와 다른 경로를 탐색하는 방식이다.
- 동작 원리
- 시작 노드에서 출발하여 한 방향으로 갈 수 있는 만큼 깊이 내려간다.
- 더 이상 내려갈 수 없으면, 마지막으로 방문한 노드로 되돌아가서 다른 경로로 탐색을 진행한다.
- 모든 노드를 방문할 때까지 이 과정을 반복한다.
- 구현 방법
- 재귀 (Recursive)
- Python은 재귀 함수 최대 깊이에 제한이 있다. (최대 1000) 만약 더 깊은 재귀 깊이가 필요하다면, sys.setrecursionlimit 을 통해 늘려주어야 한다.
- 스택 (Stack)을 사용한 반복적(Iterative) 구현
- 재귀 (Recursive)
너비 우선 탐색 (BFS)
너비 우선 탐색은 시작 노드에서 인접한 노드들을 먼저 모두 탐색한 후, 그 다음 레벨의 노드들을 탐색하는 방식이다.
- 동작 원리
- 시작 노드에서 출발하여 인접한 모든 노드를 먼저 탐색한다.
- 다음 레벨의 모든 노드를 탐색하기 전에 현재 레벨의 모든 노드를 탐색한다.
- 모든 노드를 방문할 때까지 이 과정을 반복한다.
- 구현 방법
- 큐 (Queue)를 사용한 반복적(Iterative) 구현
BOJ-24479: 알고리즘 수업 - 깊이 우선 탐색 1
- 난이도: 실버
- 분류: DFS
- 링크: 24479번: 알고리즘 수업 - 깊이 우선 탐색 1
#576ms
import sys
input = sys.stdin.readline
from collections import defaultdict
#정점의 수 n, 간선의 수 line, 시작 정점 R
node, line, start = map(int, input().split())
def dfs(start):
stack = [start]
order = 1
while stack:
current = stack.pop()
if not visited[current]:
visited[current] = True
visit_order[current] = order
order += 1
#인접 노드를 오름차순으로 방문하기 위해 sorted
for adj in sorted(graph[current], reverse=True):
if not visited[adj]:
stack.append(adj)
graph = defaultdict(list)
visited = [False] * (node + 1)
visit_order = [0] * (node + 1)
for _ in range(line):
u, v = map(int, input().split())
graph[u].append(v)
graph[v].append(u)
dfs(start)
for i in range(1, node + 1):
print(visit_order[i])
BOJ-18352: 특정 거리의 도시 찾기
- 난이도: 실버
- 분류: BFS (최단 거리)
- 링크: 18352번: 특정 거리의 도시 찾기
#1872ms
import sys
from collections import defaultdict, deque
input = sys.stdin.readline
def bfs(start):
queue = deque([start])
distance[start] = 0 #시작점의 거리는 0
while queue:
current = queue.popleft()
for neighbor in graph[current]:
if distance[neighbor] == -1: #아직 방문하지 않은 경우
distance[neighbor] = distance[current] + 1
queue.append(neighbor)
city, road, length, start = map(int, input().split())
graph = defaultdict(list)
for _ in range(road):
u, v = map(int, input().split())
graph[u].append(v)
distance = [-1] * (city + 1) #모든 도시에 대한 거리를 -1로 초기화
bfs(start)
#최단 거리가 K인 도시들을 찾아 오름차순으로 정렬
result = [i for i in range(1, city + 1) if distance[i] == length]
if result:
for city in sorted(result):
print(city)
else:
print(-1)

Comments