이분 탐색 (Binary Search)

정렬된 배열에서, 탐색 범위를 절반 씩 줄여나가는 탐색 방법이다. 절반씩 줄여나가면서 탐색 범위가 1이 될 때까지 진행하므로 시간 복잡도는 O(log n) 이며 이진 탐색 이라고도 불린다.

이분 탐색의 특성

• 빠른 검색 속도: 시간 복잡도가 O(log n)이기 때문에 매우 빠르게 값을 찾을 수 있다.
• 재귀적 접근: 재귀적으로 배열을 절반씩 나누면서 값을 찾는 방식이다.
• 정렬된 배열에서 사용: 이분 탐색은 배열이 정렬되어 있어야 사용할 수 있다.

힙과 정렬의 사용 경우

• 힙을 사용해야 하는 경우:
  • 우선 순위 큐가 필요한 상황 (작업 스케줄링, 최단 경로 알고리즘 등)
  • 실시간으로 최대값 또는 최소값을 빠르게 삽입/삭제해야 하는 상황
  • 실시간으로 중간값을 유지해야 하는 상황
• 정렬을 사용해야 하는 경우:
  • 데이터를 완전히 정렬된 상태로 유지해야 하는 상황
  • 정렬된 데이터를 기반으로 빠르게 검색해야 하는 상황
  • 특정 알고리즘의 전처리로서 데이터 정렬이 필요한 상황

정렬 (Sort)

정렬(Sort)은 데이터의 요소들을 일정한 순서에 따라 재배열하는 과정이다. 정렬 알고리즘은 다양한 종류가 있으며, 주로 비교 기반 정렬과 비교 기반이 아닌 정렬로 나눌 수 있다.

• 주요 정렬
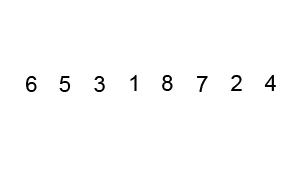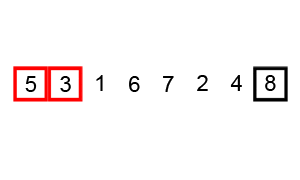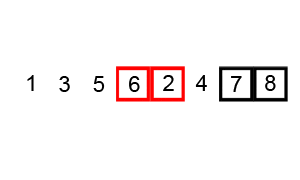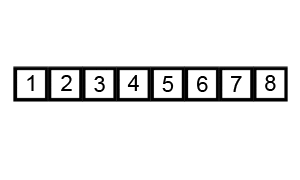
  • 버블 정렬 (Bubble Sort):
    • 인접한 두 요소를 비교하여 필요에 따라 교환하는 방식으로, 배열의 끝까지 이를 반복한다.
    • 최선의 시간 복잡도: O(n)
    • 최악의 시간 복잡도: O(n²)
  
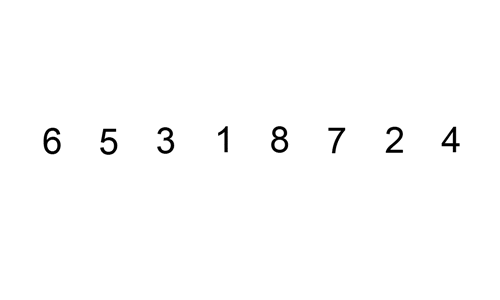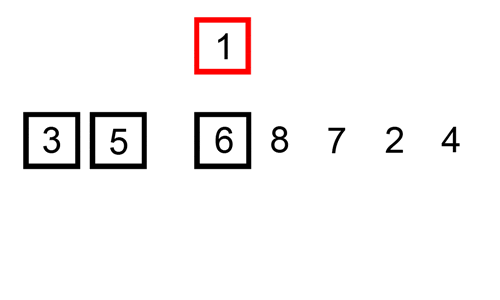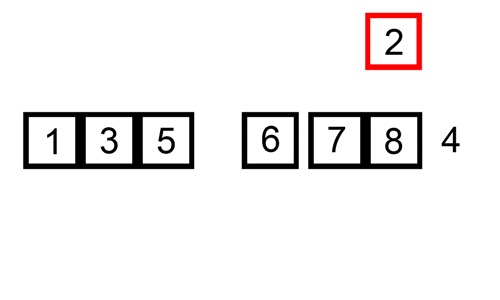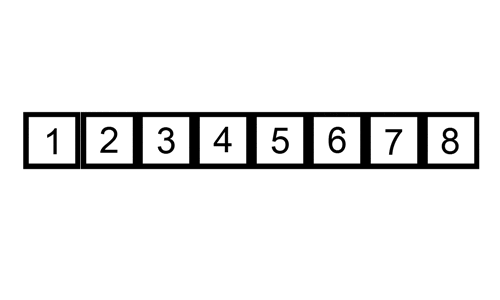
  • 삽입 정렬 (Insertion Sort):
    • 배열의 요소를 차례로 비교하여, 해당 요소를 올바른 위치에 삽입한다.
    • 최선의 시간 복잡도: O(n)
    • 최악의 시간 복잡도: O(n²)
  
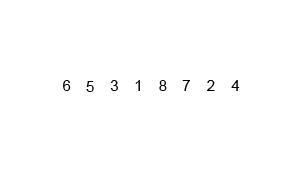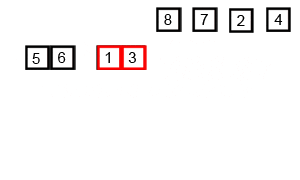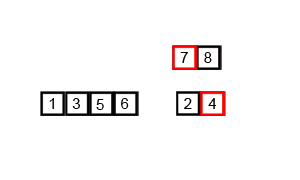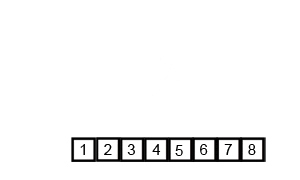
  • 병합 정렬 (Merge Sort):
    • 배열을 반으로 나누고, 각각을 정렬한 후 병합하는 정렬 방법이다.
    • 시간 복잡도: O(n logN)
    • 항상 분할 및 병합을 해야 하기 때문에 최선과 최악의 경우가 동일
  
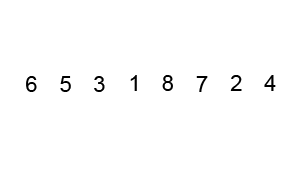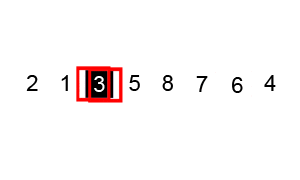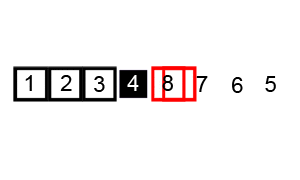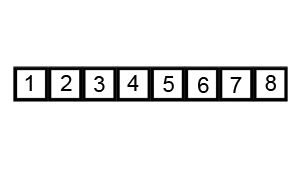
  • 퀵 정렬 (Quick Sort):
    • 기준 값을 중심으로 작은 값과 큰 값을 분리하여 정렬하는 방법이다. 재귀적으로 이 과정을 반복하여 정렬한다.
    • 최선의 시간 복잡도: O(n logN)
    • 최악의 시간 복잡도: O(n²)
  
  • 힙 정렬 (Heap Sort):
    • 힙 정렬은 힙 자료구조를 이용하여 배열을 정렬하는 효율적인 방법이다. 최대 힙이나 최소 힙을 사용하여 배열의 최대값이나 최소값을 하나씩 제거하면서 정렬한다.
    • 시간 복잡도: O(n logN)
    • 배열을 힙 구조로 만들고, 하나씩 정렬하는 과정에서 로그 시간이 걸리기 때문에 항상 위와 같은 시간이 소요됨

BOJ-18870: 좌표 압축

• 난이도: 실버
• 분류: 정렬
• 링크: 18870번: 좌표 압축

cnt = int(input())

coordinate = list(map(int, input().split()))
sortls = sorted(list(set(coordinate)))

dic = {}

for i in range(len(sortls)):
    dic[sortls[i]] = i

for i in coordinate:
    print(dic[i], end=" ")

BOJ-10815: 숫자카드

• 난이도: 실버
• 분류: 이분 탐색
• 링크: 10815번: 숫자카드

cardcnt = int(input()) #숫자카드 갯수
card = list(map(int, input().split()))

numcnt = int(input())
number = list(map(int, input().split()))

dic = {}

for i in range(cardcnt):
    dic.setdefault(card[i], 1)

for j in range(numcnt):
    print(dic.get(number[j], 0), end=" ")